Nedanstående bidrag kom in till TfS 2021/2. Redaktionen väljer att i stället publicera artikeln digitalt.
Swedish Chess Federation (SSF) was founded in 1917 and has completed 104 glorious years. Let us celebrate and commemorate it with interesting tours of knight on 8×13 (=104) cell board.
Readers may recall the ‘Tour of knight’ puzzle – view Tidskrift for Schack # 4 – 2020 p. 35. The challenge is to move a knight over an empty board so that it covers all the cells in successive jumps, without visiting any cell twice. Figure 1 is a semi-magic tour of knight on 8×13 board. Here, all the consecutive numbers from 1 to 104 are at knight’s move and sum of all the 13 columns is 420. Since it is an ‘even by odd’ size board, the number of dark and light cells in the rows are unequal. Therefore, all the rows can’t sum up to a magic constant and their sums are odd and even, alternately. A magic tour of knight has all the rows and all the columns sum up to a magic constant and it is possible only on ‘even by even’ size board.
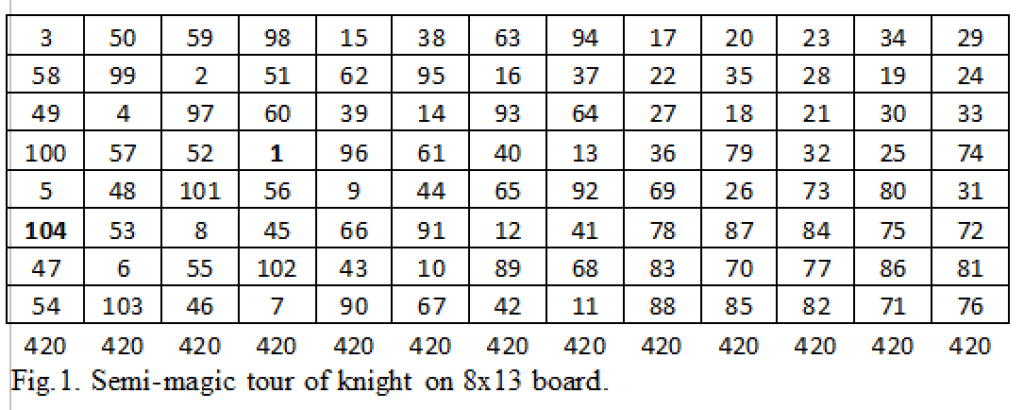
Figure 2 is a piece of art having an aesthetic appeal. It is called ‘figured tour’ of knight on 8×13 board. Tour of knight is over a millennium old puzzle but ‘figured tour’ of knight is a recent, albeit, less explored field. T. R. Dawson (1889-1951), the indefatigable English chess author, and the ‘father of Fairy Chess’, coined and popularized the term ‘Figured Tour’ in 1940’s. The name figured tour is appropriate for any numbered tour in which certain arithmetically related numbers are arranged in a geometrical pattern. Jelliss [1] has described and compiled wide varieties of Figured tours. Here, all the consecutive square numbers, namely, 1, 4, 9 …, 100 are also along knight path and the line joining them makes heart shape – the universal symbol of love. We love, adore and admire SSF. It has over 40,000 members and is doing exemplary service in promoting chess among youth and children.
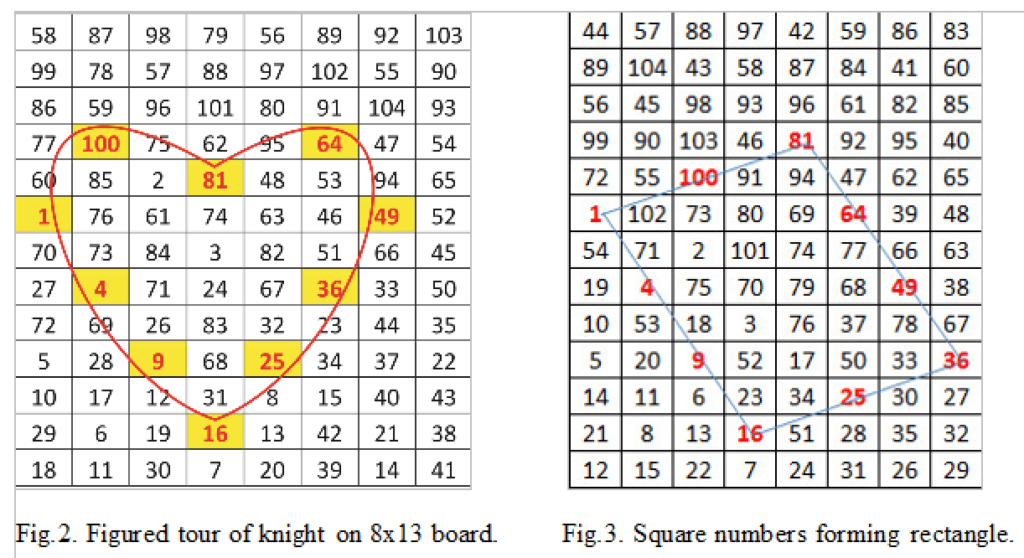
Figure 3 is a mathematical piece. Here the square numbers are forming a rectangle having an area of 30 units. It is the largest rectangle possible on 8×13 board. The author has only shown two examples – sky is the limit for figured tours.
Eagle-eyed readers must have spotted that all the tours are open tours of knight, that is, the first and the last cells of knight tour are not connected by knight move. Closed (or reentrant) knight tour is more challenging and readers are requested to compose such tours.
Once again, congratulations to Swedish Chess Federation for completing 104 glorious years and we wish to celebrate its bicentenary. Amen.
Reference: G.P. Jelliss; Figured Tours – A Mathematical Recreation, available at www.mayhematics.com.
Awani Kumar, Lucknow, INDIA






